Research Article - (2015) Volume 3, Issue 1
Keywords: Climate data; Correlation; Simple regression; Multiple regression
Climate is a measure of the average pattern of variation in temperature, humidity, atmospheric pressure, wind, precipitation, atmospheric particle count and other meteorogical variables in a given region over long periods of time. Climate is different from weather, in that weather only describes the short-term conditions of these variables in a given region.
Climate is a critical factor in the lives and livelihoods of the people and socio-economic development as a whole. India has to face the challenge of sustaining its rapid economic growth in the era of rapidly changing global climate. The problem has emanated from accumulated greenhouse gas emissions in the atmosphere, anthropogenically generated through long-term and intensive industrial growth and high consumption lifestyles in developed countries. Though, there is need to continuously engage international community to collectively and cooperatively deal with this threat, India needs a strong national strategy to firstly, adapt to climate change and secondly, to further enhance the ecological sustainability of its development path. This path is based on its unique resource endowments, the overriding priority of economic and social development and poverty eradication, and its adherence to its civilization legacy that places a high value on the environment and the maintenance of ecological balance. The national vision is to create a prosperous, but not wasteful society, an economy that is self-sustaining in terms of its ability to unleash the creative energies of our people and is mindful of our responsibilities to both present and future generations. This is in tune with global vision inspired by Mahatma Gandhi’s wise dictum - “The earth has enough resources to meet people’s needs, but will never have enough to satisfy people’s greed”. As such, promotion of sustainable production processes along with but equally, sustainable lifestyles across the globe should be the focus point of our efforts.
The climate is a dynamical system influenced not only by immense external factors, such as solar radiation or the topography of the surface of the solid Earth, but also by seemingly insignificant phenomenon. If we know all these factors, and the state of the full climate system (including the atmosphere, the ocean, the land surface etc.), at a given time in full detail, then there would not be room for statistical uncertainty. We do not know all factors that control the trajectory of climate in its enormously large phase space. Thus it is not possible to map the state of atmosphere, the ocean, and the other components of the climate system in full detail. Also, the models are not deterministic in a practical sense: an insignificant change in a single digit in the model’s initial conditions causes the model’s trajectory through phase space to diverge quickly from the original trajectory. Therefore, in a strict sense, we have a ‘deterministic’ system, but we do not have the ability to analyse and describe it with “deterministic’ tools. Instead, we use probabilistic ideas and statistics to describe the ‘climate’ system. The climate is controlled by innumerable factors. Only a small proportion of these factors can be considered, while the rest are necessarily interpreted as background noise. The details of the generation of this ‘noise’ are not important, but it is important to understand that this noise is an internal source of variation in the climate system.
Many researchers studied various problems related to climate systems. Box and Jenkins [1] suggested time series model for hydrological forecasting. These models include: Auto Regressive Integrated Moving Average (ARIMA), Auto Regressive Moving Average (ARMA), Auto Regressive (AR), and Moving Average (MA). Burlando et al., [2] used ARMA model for forecasting of short-term rainfall [3]. Valipour et al., [4] made comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir [5]. Number of required observation data for rainfall forecasting according to the climate conditions was studied by Valipour [6,7]. The estimation of parameters of ARIMA and ARMA models studied by Valipour et al., [8]. Mohammadi et al., [9] used goal programming for parameter estimation of an ARMA model for river flow forecasting. Analysis of potential evapotranspiration using limited weather data.Study of different Climatic conditions to assess the role of solar radiation in reference crop evapotranspiration equations is attempted by Valipour [10,11]. A case study is given by Valipour [12] to see the ability of Box-Jenkins model to estimate of reference potential evapotranspiration.
The paper is arranged as follows. In section 4, the concept of mean and correlation is discussed. In section 5, simple linear regression model is represented. In section 6, the multiple regression model is considered. In section 7, a numerical example depend on secondary data is considered to explain above statistical tools. Conclusions are made in last section [8].
The mean climate state
From the point of view of the climatologist, the most fundamental statistical parameter is the mean state. This seemingly trivial animal in the statistical zoo has considerable complexity in the climatological context. The computed mean is not entirely reliable as an estimate of the climate system’s true long-term mean state. The computed mean will contain error caused by taking observations over a limited observing period, at discrete times and a finite number of locations. It may also be affected by the presence of instrumental, recording, and transmission errors. In addition, reliability is not likely to be uniform as a function of location [13].
Correlation
In the statistical lexicon, the word correlation is used to describe a linear statistical relationship between two random variables. The phrase ‘linear statistical’ indicates that the mean of one of the random variables is linearly dependent upon the random component of the other. The stronger relationship indicates the stronger correlation. A correlation coefficient of +1(-1) indicates a pair of variables that vary together precisely, one variable being related to the other by means of a positive (negative) scaling factor.
Simple Regression Model
Let Y be the dependent variable and X be the independent variable. Let , y1 , y2 ... yn be n- observations recorded on Y variable. Let , x1 ,x2 .... xn be n- observations recorded on X variable. Under the assumptions of linear relationship between Y and X, simple regression model of Y on X is as below:
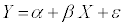 (1)
(1)
The unknown parameters α and β are to be estimated by ethod of least square ( i.e. by minimizing residual sums of squares (S)).The random (noise) factor (ε) is assumed to follow normal distribution with mean zero and unit standard deviation. The estimate of α and β are obtain by considering function 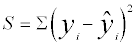 , which is to be minimized. The estimate of α and β are obtain by solving partial derivatives
, which is to be minimized. The estimate of α and β are obtain by solving partial derivatives 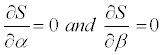 respectively, which are given below:
respectively, which are given below:
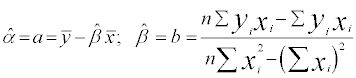
Multiple regression model is used to study more than two variables. Let X1, X2,....,Xk be k-variables under study. The regression model of three variables, by assuming X1 dependent and other independent variables, can be written as below:
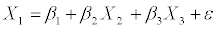 (2)
(2)
The unknown parameters β1, β2 and β3 are to be estimated by method of least square ( i.e. by minimizing residual sums of squares (S)).The random (noise) factor (ε) is assumed to follow normal distribution with mean zero and unit standard deviation.
Let n-observations are recorded on the variables X1, X2, and X3. The total correlation coefficient denoted as r12,r13 and r23, are calculated by using following formula,
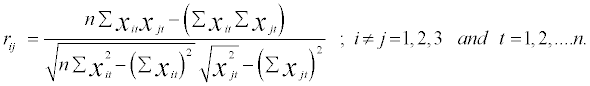
The sample variances 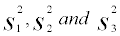 are obtain by using following formula,
are obtain by using following formula,
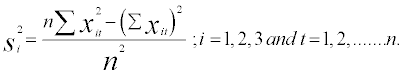
The correlation matrix for three variables is given below:
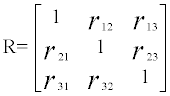
The cofactor of (i,j)th element of determinant of matrix R is defined as below:
Rij=(-1)i+j minor of element(i,j) i= 1,2,3, and j=1,2,3.
The estimates β1, β2 and β3 are obtain by considering function 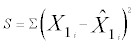 , which is to be minimized. The estimates of β1, β2 and β3 are obtain by solving partial derivatives
, which is to be minimized. The estimates of β1, β2 and β3 are obtain by solving partial derivatives 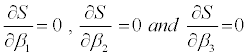 respectively. The estimates are given as below:
respectively. The estimates are given as below:
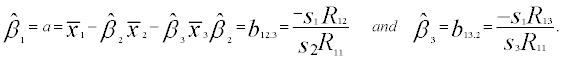
The fitted model for equation (2) is X1=a + b12.3X2 + b13.2X3 and is used to find estimate of X1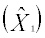
for given X2 and X3. The reliability of fitted model to (2) is checked by calculating residual (Y-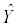 )
)
The secondary data is taken from the India Meteorological Department [14]. The data contains information about mean maximum temperature, mean minimum temperature and mean rain fall for the year 1901 to 2000 ( i.e 100 years). The data for Pune city is given below (Table 1).
| Month | Temperature in centigrade | Rainfall in mm | |
|---|---|---|---|
| Maximum | Minimum | X1 | |
| X2 | X3 | ||
| Jan | 30.2 | 11.6 | 1.6 |
| Feb | 32.3 | 12.7 | 1.1 |
| Mar | 35.8 | 16.3 | 2.7 |
| Apr | 37.9 | 20.1 | 13.6 |
| May | 37.2 | 22.3 | 33.3 |
| Jun | 32 | 22.8 | 120.4 |
| Jul | 28.1 | 22 | 179 |
| Aug | 27.6 | 21.3 | 106.4 |
| Sep | 29.2 | 20.6 | 129.1 |
| Oct | 31.7 | 18.9 | 78.8 |
| Nov | 30.5 | 14.8 | 28.6 |
| Dec | 29.3 | 11.8 | 5.3 |
Table 1: Monthly mean maximum and minimum temperature & total rainfall based upon 1901 to 2000 data (Place: Pune).
The correlation coefficient between three variables are calculated and given as below:
r12 =− 0.5189 ; r13=0.7309 .
It concludes that the variable rainfall and the variable mean minimum temperature has strong correlation than with variable mean maximum temperature. So, the pair ( X1, X3) will be effective for further analysis. This can be explained by ANOVA analysis (Table 2).
| Summary Output | ||||||
|---|---|---|---|---|---|---|
| Regression | Statistics | |||||
| Multiple R | 0.5188577 | |||||
| R Square | 0.2692133 | |||||
| Adjusted R Square | 0.1961346 | |||||
| Standard Error | 55.443273 | |||||
| Observations | 12 | |||||
| ANOVA | ||||||
| Source of variation | df | SS | MS | F | Significance F | |
| Regression | 1 | 11324.09755 | 11324.1 | 3.683883 | 0.083899789 | |
| Residual | 10 | 30739.56495 | 3073.956 | |||
| Total | 11 | 42063.6625 | ||||
| Coefficients | Standard error | t Stat | P-value | |||
| Intercept | 353.85107 | 154.8020023 | 2.28583 | 0.045322 | ||
| X Variable 3 | -9.2884044 | 4.839362702 | -1.91934 | 0.0839 | ||
Table 2: Simple linear regression analysis of X1 and X2.
Simple linear regression model of X1 on X2=353.85107-9.2884X2+ε
As P-value=.0839>0.05 ⇒ Variable mean maximum temperature may not have enough impact on rainfall (Table 3).
| Summary Output | ||||||
|---|---|---|---|---|---|---|
| Regression | Statistics | |||||
| Multiple R | 0.730872 | |||||
| R Square | 0.5341739 | |||||
| Adjusted R Square | 0.4875913 | |||||
| Standard Error | 44.265508 | |||||
| Observations | 12 | |||||
| ANOVA | ||||||
| Source of variation | df | SS | MS | F | Significance F | |
| Regression | 1 | 22469.31083 | 22469.3108 | 11.46724 | 0.006928443 | |
| Residual | 10 | 19594.35167 | 1959.43517 | |||
| Total | 11 | 42063.6625 | ||||
| Coefficients | Standard Error | t Stat | P-value | |||
| Intercept | -131.2993 | 57.43645068 | -2.2859918 | 0.045322 | ||
| X Variable 3 | 10.573843 | 3.1225071 | 3.38633116 | 0.006928 | ||
Table 3: Simple linear regression analysis of X1 and X3.
Simple linear regression model of X1 on X3=-131.2993+10.5738X3+ε
As P-value=.006928
Add one more variable as range (difference between max. temp. and min. temp.) in the data, so modified data is given in table below (Table 4).
| Month | Temperature in centigrade | Rainfall in mm | ||
|---|---|---|---|---|
| Maximum | Minimum | Range | X1 | |
| X2 | X3 | X4 | ||
| Jan | 30.2 | 11.6 | 18.6 | 1.6 |
| Feb | 32.3 | 12.7 | 19.6 | 1.1 |
| Mar | 35.8 | 16.3 | 19.5 | 2.7 |
| Apr | 37.9 | 20.1 | 17.8 | 13.6 |
| May | 37.2 | 22.3 | 14.9 | 33.3 |
| Jun | 32 | 22.8 | 9.2 | 120.4 |
| Jul | 28.1 | 22 | 6.1 | 179 |
| Aug | 27.6 | 21.3 | 6.3 | 106.4 |
| Sep | 29.2 | 20.6 | 8.6 | 129.1 |
| Oct | 31.7 | 18.9 | 12.8 | 78.8 |
| Nov | 30.5 | 14.8 | 15.7 | 28.6 |
| Dec | 29.3 | 11.8 | 17.5 | 5.3 |
Table 4: Difference between maximum temperature and minimum temperature and add one more variable as range.
The correlation coefficient between four variables are calculated and given as below:
r12 =−0.5189 ; r13 =0.7309 ; r14=−0.9603.
It shows that there is strong correlation between range and rainfall, so it says that the prediction of rainfall with variable range may be more informative than other two variables. Smaller the range says the more chance of rainfall. This can be verified by ANOVA (Table 5).
| SUMMARY OUTPUT | ||||||
|---|---|---|---|---|---|---|
| Regression | Statistics | |||||
| Multiple R | 0.96024691 | |||||
| R Square | 0.92207413 | |||||
| Adjusted R Square | 0.91428155 | |||||
| Standard Error | 18.1048262 | |||||
| Observations | 12 | |||||
| ANOVA | ||||||
| Source of variation | df | SS | MS | F | Significance F | |
| Regression | 1 | 38785.81518 | 38785.82 | 118.3271 | 7.31326E-07 | |
| Residual | 10 | 3277.847316 | 327.7847 | |||
| Total | 11 | 42063.6625 | ||||
| Coefficients | Standard Error | t Stat | P-value | |||
| Intercept | 219.345168 | 15.69816974 | 13.97266 | 6.90003E-08 | ||
| X Variable 3 | -11.598091 | 1.066214104 | -10.8778 | 7.31326E-07 | ||
Table 5: Simple linear regression analysis of X1 and X4
Simple linear regression model of X1 on X4=219.3452-11.5981X4+ε
As P-value=7.31326E-07 <<<<0.05 ⇒Variable mean range temperature may have stronger impact on rainfall (Table 6).
| SUMMARY OUTPUT | ||||||
| Regression | Statistics | |||||
| Multiple R | 0.960573218 | |||||
| R Square | 0.922700908 | |||||
| Adjusted R Square | 0.905523332 | |||||
| Standard Error | 19.0072586 | |||||
| Observations | 12 | |||||
| ANOVA | ||||||
| Source of variation | df | SS | MS | F | Significance F | |
| Regression | 2 | 38812.17958 | 19406.09 | 53.71543 | 9.92624E-06 | |
| Residual | 9 | 3251.482917 | 361.2759 | |||
| Total | 11 | 42063.6625 | ||||
| Coefficients | Standard Error | t Stat | P-value | |||
| Intercept | 204.9586912 | 55.74734782 | 3.676564 | 0.005103 | ||
| X Variable 2 | -11.2616988 | 1.674400111 | -6.72581 | 8.6E-05 | ||
| X Variable 3 | 11.80349582 | 1.353187306 | 8.722736 | 1.1E-05 | ||
Table 6: Multiple Regression model between X1 on X2 and X3.
Multiple correlation of X1 with X2 and X3=0.960573
Multiple correlation of X1 with X3 and X4=0.960573
Multiple correlation of X1 with X2 and X4=0.960573
Multiple correlation of X1 with X2, X3 and X4=0.960573
From above calculation, it concludes that in multiple regression adding functional variable (range) does not change value of multiple correlation coefficient. So, we study multiple regression only by original variables as below:
Multiple regression model between X1 on X2 and X3=204.9587-11.2617X2+11.8035X3+ε
As P-value for mean maximum temperature=8.6E-05<
As P-value for mean minimum temperature=1.1E-05<<<
Comparison of various simple regression models based on residuals
Comparison of various simple regression models based on Residuals are given in Tables 7-10.
| Observation | Predicted Y | Residuals |
|---|---|---|
| 1 | 73.34125378 | -71.7412538 |
| 2 | 53.83560454 | -52.7356045 |
| 3 | 21.32618915 | -18.6261891 |
| 4 | 1.820539909 | 11.77946009 |
| 5 | 8.322422988 | 24.97757701 |
| 6 | 56.62212586 | 63.77787414 |
| 7 | 92.84690301 | 86.15309699 |
| 8 | 97.49110521 | 8.908894786 |
| 9 | 82.62965818 | 46.47034182 |
| 10 | 59.40864718 | 19.39135282 |
| 11 | 70.55473246 | -41.9547325 |
| 12 | 81.70081774 | -76.4008177 |
| Total | 2.55795E-13 |
Table 7: Comparison of various simple regression models based on Residuals.
| Observation | Predicted Y | Residuals |
|---|---|---|
| 1 | -8.642672914 | 10.2426729 |
| 2 | 2.988554487 | -1.8885545 |
| 3 | 41.05438962 | -38.35439 |
| 4 | 81.23499337 | -67.634993 |
| 5 | 104.4974482 | -71.197448 |
| 6 | 109.7843697 | 10.6156303 |
| 7 | 101.3252952 | 77.6747048 |
| 8 | 93.92360508 | 12.4763949 |
| 9 | 86.52191491 | 42.5780851 |
| 10 | 68.54638166 | 10.2536183 |
| 11 | 25.19362498 | 3.40637502 |
| 12 | -6.527904296 | 11.8279043 |
| Total 2.7001E-13 |
Table 8: Residual output for model X1 on X3.
| Observation | Predicted Y | Residuals |
|---|---|---|
| 1 | 3.620669125 | -2.020669125 |
| 2 | -7.977422226 | 9.077422226 |
| 3 | -6.817613091 | 9.517613091 |
| 4 | 12.89914221 | 0.700857794 |
| 5 | 46.53360713 | -13.23360713 |
| 6 | 112.6427278 | 7.75727217 |
| 7 | 148.596811 | 30.40318898 |
| 8 | 146.2771927 | -39.87719275 |
| 9 | 119.6015826 | 9.498417359 |
| 10 | 70.88959896 | 7.910401036 |
| 11 | 37.25513404 | -8.655134045 |
| 12 | 16.37856961 | -11.07856961 |
| Total | 1.3145E-13 |
Table 9: Residual output for model X1 on X4.
| Observation | Predicted Y | Residuals |
|---|---|---|
| 1 | 1.775939496 | -0.1759395 |
| 2 | -8.88978255 | 9.989782546 |
| 3 | -5.81314333 | 8.513143329 |
| 4 | 15.39057335 | -1.79057335 |
| 5 | 49.2414533 | -15.9414533 |
| 6 | 113.7040349 | 6.695965111 |
| 7 | 148.1818635 | 30.81813651 |
| 8 | 145.5502658 | -39.1502658 |
| 9 | 119.2691007 | 9.830899326 |
| 10 | 71.04891082 | 7.751089181 |
| 11 | 36.16861649 | -7.56861649 |
| 12 | 14.27216757 | -8.97216757 |
| Total | 9.5568E-13 |
Table 10: Residual output for multiple regression model X1 on X2 and X3.
It is observed that the correlation between rainfall and mean minimum temperature is positive and significant than with mean maximum temperature. Also, the correlation between rainfall with range temperature shows stronger impact than other two variables. By ANOVA, it observed that simple regression model of rainfall on range temperature is more significant than others. The multiple regression model of rainfall on mean maximum temperature and mean minimum temperature gives better estimate. Range temperature factor does not alter the result in multiple regression analysis. Hence, I suggest to estimate rainfall by multiple regression model. It is possible to improve analysis by adding some other factors to improve estimation. Some Greenhouse gases, which are responsible for increment of temperature, may be considered in the analysis.
The author would like to express the gratitude to the anonymous reviewers whose constructive and insightful comments have led to many improvements of this paper.