Journal of Climatology & Weather Forecasting

We know that a cyclone when entering a land mass slowly reduces its energy as favorable parameters for its development are being stopped and ultimately it dies out. But few have tried to study the effect of its reduction of energy by the varied landforms. In this paper a humble attempt has been made to study the effect of an inclined plane on the reduction of energy of the cyclone and it has been shown mathematically that when a cyclone traverses an inclined plane then it dissipates it’s energy more faster compared to the cyclone traversing the plane land assuming their energy content being same. This assumption has a sound footing as we know that all the favorable parameters required for development of the cyclone is cut off.

We suppose that an spherical parcel of air of mass “m_rz” is rotating having a tangential velocity “V₁” due to the average pressure gradient “ P “ w.r.t the centre of the cyclone in the plane in which the spherical parcel of air mass lies (Figure 1). Then according to equation 1 [1]. A method has been devised to find the area of the curve by interchange in ( x,y) co-ordinate system with the axis by integration method (Figure 2).

Figure 1: Digrammatic representation to find the pressure gradient.

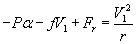(1)

If we consider the left hand side of the circulation assuming the air parcel to be of unit mass. (Figure 1)

{Coriolis force f = 2Ω Sin Ø where Ø is the latitude of the place and Ω is the angular velocity of the earth at that latitude }

(Also α is the cross section area of spherical parcel of air of unit mass mrz on which P acts normally, F_r is the force of friction, “z” is the height of this parcel from the level of the ground and r is the radial vector at which the air parcel mrz lies ).

Now from equation 1 it can be further derived that when the axis of rotation of the cyclone inclines by an angle θ for cyclone climbing an inclined plane at an angle θ. Then we can write

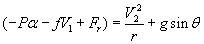(2)

or

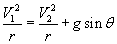(3)

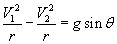( for 0 < θ < 90 )

Therefore V₁>V₂ as 0<θ<90, except V₁=V₂ when θ=0

This shows that as the radial force towards the centre is constant so to maintain dynamic equilibrium the tangential velocity changes accordingly.

Similarly we can prove that V₃ >V₁ as follows

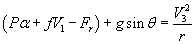(3) as radial force towards the centre is constant

as 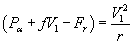if we consider the left hand side of the circulation in the Figure 1.

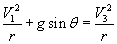(4)

or

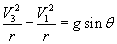
i.e V₃>V₁ as 0<θ1=V₃ when θ=0

Also Energy ‘ E _V1 ‘ possessed by the infinitesimal spherical air mass ‘mrz ‘ positioned at a perpendicular distance “r” from the axis of rotation at a height “z” from the level of the ground and rotating at angular velocity ω₁ ( where ω₁=V₁ ) is

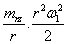
As 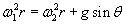----- from Eq.3, since v = ωr

or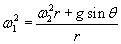

So the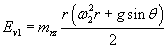

or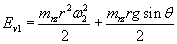

or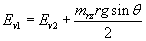

i.e 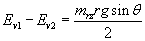(4)

i.e. Energy will be reduced when the mrz rotating in the horizontal plane with tangential velocity _V1 drops down to the inclined plane and starts rotating in the horizontal plane with tangential velocity _V2. Similarly energy will be gained when the mrz rotating in the horizontal plane with tangential velocity _V1 rises up the inclined plane and starts rotating in the horizontal plane with tangential velocity _V3.

The total energy reduced by the vertical slice portion (lower the horizontal plane) or gained (higher the horizontal plane) by half the cyclone volume will be

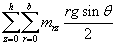
or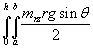

The ‘h’ being the height of the cyclone and ‘a’ being the inner radius and ‘b’ being the outer radius of the cyclone (Figure 1).

Also as in a cyclone air mass is in dynamic motion against a essentially a two form of fluid system, fluid mechanics and particle transport equations can be used to describe the behaviour of a cyclone [2-5]. We have already assumed the tangential velocity of the spherical air mass in the horizontal plane is _V1 and assume further that the radial velocity be Vr at the radius r, then assuming Stoke’s law, the drag force on any particle moving tangentially in a cyclic path is given by the following equation.

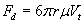(5)

F_d is the frictional force acting on the interface between the fluid and the particle (in N),

μ is the dynamic viscosity (N s/m²),

r is the radius of the spherical object (in m), and

V_t is the particle’s tangential velocity (in m/s).

If one considers an isolated particle circling in the cylindrical component of the cyclone at the rotational radius of r from the cyclone’s central axis , the particle will experience the centrifugal force F_c which counteracts the force m(-Pα - f_V1 + F_r ) and is equal to mrz _V1²

i.e. 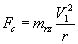(6)

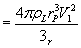
where ρ_L is the density of lighter spherical air mass and r_p is the radius of the lighter spherical parcel of air mass.

The buoyant force component is obtained by the difference between the lighter air mass and denser air mass which are denoted by ρ_L and ρ_D respectively :

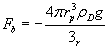
The force balance can be created by summing the forces together.

i.e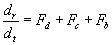

This rate is controlled by the radius of the revolving air mass around the central axis of the cyclone. A spherical air mass in the cyclone flow will move towards either towards the wall of the cyclone or the central axis of cyclone until the drag, the uplift and the centrifugal forces are balanced. Assuming the system has reached a steady state, the particles will assume a characteristic radius dependent upon the force balance [6-9]. Heavier, denser particles will assume a solid flow at some larger radius than the light particles. The steady state balance assumes that for all particles, the forces are equated, hence

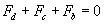
Which expands to

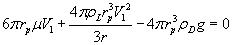
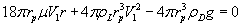
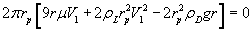
i.e. it is a quadratic equation of _V1 and gives

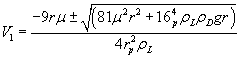
Thus we see that _V1 α r, as other are fixed quantities.

Hence when tangential velocity decreases (i.e._V2 ) the radius of the cyclone decreases which subsequently will increase the centrifugal force but as force balance has to be maintained in the dynamic equilibrium so the drag force and buoyant force will decrease. Similarly when tangential velocity increases (i.e. _V3) the radius of the cyclone increases which subsequently will decrease the centrifugal force but as force balance has to be maintained in the dynamic equilibrium so the drag force and buoyant force will increase. Thus we see that the three forces i.e Fd, Fc & Fb, for the plane of rotating air mass whose inclination lies below the horizontal plane behaves in opposing manner for the plane of rotating air mass whose inclination lies above the horizontal plane. This will trigger wobbling of the system and ultimately the system will die out early compared to smooth horizontal rotation. This is supported by the fact that the Tropical Cyclone (TC) whose intensity during landfall which is proportional to Mean Surface Wind (MSW) speed, is same (i.e. MSW is 65 knot marked in blue color in Figure 3) dies out after moving through less distance (13.875 km) when traversing through relatively steep landforms areas which tilts the axis of the TC than gentle slopes where MSW during landfall is 65 knot but moves through after traveling 101 km, 111 km and 41.625 km respectively (Figures 4-6). The color coded landform scale given below the map specifies the varying altitudes of the land and we can get a idea of the slopes. It is also seen that the TC with more intensity as in Figure 7 where MSW is 135 knot during landfall, marked in red color, also dies out after moving through 20.183 km compared to lower intensities when traversing through steep slopes. This proves the assertion that cyclones whose axis gets tilted more dissipates its energy faster than less tilted cyclones.

Figure 2: Method to find the area of the curve by interchange in (x,y) coordinate.

Figure 3: JAXA/EORC Tropical Cyclone Database Japan Aerospace Exploration Agency Earth Observation Research Center JAXA/EORC.

Figure 4: JAXA/EORC Tropical Cyclone Database Japan Aerospace Exploration Agency Earth Observation Research Center JAXA/EORC.

Figure 5: JAXA/EORC Tropical Cyclone Database Japan Aerospace Exploration Agency Earth Observation Research Center JAXA/EORC.

Figure 6: JAXA/EORC Tropical Cyclone Database Japan Aerospace Exploration Agency Earth Observation Research Center JAXA/EORC JAXA/EORC.

Figure 7: JAXA/EORC Tropical Cyclone database Japan Aerospace Exploration Agency Earth Observation Research Centre JAXA/EORC.

To find the length of the arc of the circle if vertical angle is known or vice versa.

Abstract : In this method a formula has been derived for finding the length of the arc of the circle by knowing the vertical angle or to find the vertical angle if the length of the arc is known. This will help to find the length of the arc or vertical angle for any point on the circle and can form a general formula.

Theory: Consider a circle of any radius and two perpendicular diameters CD and AB. By vertical angle α we mean the angle that line AP makes with straight line AOB. The arc length, by taking COD as the reference line , can be found out from the following method.

As we know the circumference which encircles 3600 is of length 2πr where r is radius. Therefore if we take COD as reference line then arc CAD and CBD encircles 1800 each i.e. the length of arc CAD or CBD is 2πr/2 = πr so each degree from centre subtends an arc length πr/180. Also as AOB is perpendicular bisector of COD therefore triangle CAD is isosceles triangle and as ∠ CAD is an angle in a semicircle hence 900 (from cyclic property) therefore ∠ CAO = 450 and ∠ DAO = 450.

Therefore to find the arc length from the reference line COD for any vertical angle say α in this case. The angle subtended by the arc at the circumference becomes (α – 45). So the angle subtended by the same arc at the centre becomes 2 (α – 45) (from cyclic property ). Hence the arc length above below the reference line COD for α>45 and α<45 respectively is given by π r X 2 (α – 45 )=π r X (α – 45 ).

It may be noted for α>45 then arc length will be +ve and for α<45 it will be -ve. The sign factor has been craftily introduced to find the vertical angle if the arc length with relevant sign is being put. We can also find the arc length of the other side if the vertical angle on the other side is known.

To find the interchanging area of the curve in (x,y) coordinate system with the axis by integration method.

Abstract: A method has been devised to find the area of the curve by interchange in ( x,y) co-ordinate system with the axis by integration method (Figure 2).

Let a function y=f (x) such that x=φ (y) and for x=a , y=f (a). and for x=b , y=f (b).

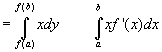
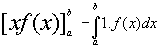
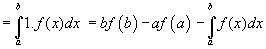
Thus we see that when the axis of cyclone tilts then for the same energy possessed by the cyclone when it is not tilted which is the case especially when the cyclone enters the land and traverses the slopes, then it dies out earlier in comparison to the non-tilted cyclone. It also proves the fact as to why the low pressure area having a vertical column tilted does not get stronger as compared to straight vertical columns which gets converted to depression. This will help in analyzing the tracks of cyclone when it traverses the landforms especially in the light of inclination of land.