Research Article - (2013) Volume 2, Issue 1
Background: Autism is a complex disorder characterized by the involvement of multiple loci in the genome and genes. Our newly described methodology, Linkage ordered Gene Sets finds pathways important in complex diseases using genomic distances. We wanted to test whether such a derivation is biased because of the distribution of the underlying microsatellite loci. Further, we also describe in this paper the detailed design underpinning LoGS.
Method: We derived a metric that tests whether the distribution of immune function genes (our primary finding in autism via LoGS) in the genome is biased in terms of the underlying microsatellite distribution. We also describe the design and working of LoGS.
Results: Our results show that there is no bias for immune function either in the 29 loci that were used in our LoGS analysis as well as 30 randomly drawn loci repeated 1000 times.
Conclusion: LoGS is a powerful methodology to probe the mechanisms underlying complex disorders. Our prior findings in autism are not emanating from any bias in the analysis introduced by LoGS.
Keywords: Autism; Genetic linkage analyses; Biological pathways; Linkage ordered gene sets
In a recent paper, we have shown that immune function can play an important role in autism [1]. Autism spectrum disorder is a neurodevelopmental disease and its incidence has been rising. It is a highly heterogeneous and complex disorder. Despite considerable work, including linkage and genome-wide association studies, its genetic causes are unknown. In Mendelian disorders, various pedigree analyses point to the same locus. However, such analyses in autism have mapped to different genetic loci, possibly a reflection of its complex nature. Single gene approaches may fail to find underlying mechanisms in such a complex disease whereas an integrative approach might succeed. We present here a detailed description of the derivation of LoGS which reflects such an integrative approach. LoGS can overcome the limitations of non-pathway-based approaches.
Non-pathway-based Methodologies in Autism (bold), their Drawbacks, and LoGSdesign (solution):
Complex disorders are studied as extensions of Mendelian disorders (the search is for multiple loci rather than one locus [2]). However, even when multiple loci are allowed, the search focuses on one gene per locus [3]. Complex disorders are multigenic by definition. If multiple genes are allowed spread across different loci [2], there is no reason to have one gene per locus. Secondly, across several loci, researchers often look for the highest significance locus [2]. If we pick only one locus (and some gene from that locus--usually the closest gene Folkersen [4] we are biasing toward one locus and discarding everything else. Solution: We therefore pick several genes on either side of any given locus. Some of these genes will be relevant (‘signal’) and some of them will not be (‘noise’).
As in Mendelian disorders, researchers may propose a gene and then pick markers within it and look for linkage [5,6]. This may provide some clues to a disease if linkage is found but may fail to identify other more important causes. Further, other than the researchers’ belief in the relevance of that gene to the disease, there is no unbiased reason to pick that gene. Solution: We thus take an unbiased approach as described below.
Linkage studies in general yield a relatively large region of uncertainty and no single gene can be identified [7]. For eg, Badner [8] says “evidence for a linkage can occur over a broad region (20-30 cM)”. Thus, people may simply identify a broad region and leave it at that [9]. The drawback is that we have no further functional understanding of the disease. One or more genes within those regions could be causative. We need some way of identifying such a gene(s). Solution: We thus collect all genes within a window that encompasses this broad region (we choose the largest possible window 50cM on each side of a locus because that is the limit of linkage and because choosing it allows the largest number of genes that may be responsible). Next we need some way to apply significance to each gene within the windows around all loci.
Sometimes researchers simply pick from within these genes one that may have functional relevance to the disease they study [3,10]. Cherry picking a gene based only on the researcher’s belief from among several next to a locus is problematic for the same reason that picking a gene and then conducting linkage is problematic. There is no reason other than the researcher’s belief that that gene may have significance. Thus, such a choice is somewhat arbitrary. See 5 for design solution.
Researchers typically pick the closest gene to a marker. For eg, “Genes in close proximity to these risk-SNPs are often thought to be pathogenetically important based on their location alone”. Others pick the closest gene to CNVs or SNPs [11]. However, non-close genes may also be important [4] we summarize the rationales here for completeness (for more details along with a pictorial description, A genomic disruption may influence non flanking genes [12-14]. Kleinjan [12] says that a region within an intron of one gene (LMBR1) has enhancers and repressors for another gene (SHH) and a third gene sits between these two (RNF32). An insertion (Sasquatch) removes the repression while a deletion (archeiropodia) disrupts the enhancer activity. It is known that microsatellites can reside in introns [15]. Thus, if a microsatellite picked such a type of deletion or insertion as a signal in a disease, that signal would not only not be pointing to the gene containing the signal or even the next closest gene, but rather a gene sitting two genes away[13].
Other drawbacks of picking the closest gene are: a. Microsatellite marker density in pedigree analysis is low and thus the signal for the correct location affecting the disease may arise at a distance from the marker. Risch used 346 markers. The human genome has about 20,000 genes (averaging 10-15 Kb in size [16]). Microsatellites on average are thus spaced 50 genes apart. Thus the closest gene to a marker may not be the causative gene. Similar considerations at a different scale occur with much higher density markers more typical of GWAS [17]. b. A corollary of the above is that we don’t have the resolution to pick a small region such as that defined by a single gene. c. There is no reason to believe that even for loci with single genes, the closest gene is important. Other non-flanking genes may also be important as pointed out earlier in this section. d. Further, there is a 30cM ambiguity (15cM on either side) about where the locus of a disease itself is located [2].
Solution: Although a locus (and its marker) may affect a nonflanking gene, it (possibly via some regulatory region) more likely asserts its influence closer by than further out (the frequency of one type of regulatory element enhancers goes down as we move away from transcription start sites [18]. Taken together with point 1 above where multiple genes are allowed, the preceding argument rationalizes ranking genes by a score. This score depends inversely on the genetic distance, d, of the gene from the marker. Thus, our metric is d-1. Another rationale is provided by a linkage perspective from a pedigree analysis. Linkage implies relevance of a gene. Closer genes are more linked and thus show more relevance (or ‘signal’) than distal genes. We thus create a ranked list of genes from each locus using d-1.
When the density is increased with SNP based analyses, the goal still is to find significant SNP(s) (and genes containing or closest to, them) [19]. The problem still remains that if we allow for multiple markers in the form of SNPs spread across the genome, why would each SNP point to one gene or the closest gene? As mentioned above, even when the density allows for one marker per gene, that marker itself can influence non flanking distal genes Folkersen [4]. Solution: We thus incorporate marker significance in our above defined ranking metric since we are taking multiple genes from multiple loci (thus in essence combining the loci). Each locus’ significance is defined by its LOD score. This new metric is our signal metric‘s’ given by LOD*d-1. Combining all loci incorporates information from all pedigrees in our analysis, and gives us a ranked list of genes.
If the loci are close enough, researchers may show that the loci are picking up the same region. In other words, the two loci are essentially collapsed into one locus [2]. This is akin to finding a significant locus (and then possibly looking for one gene) rather than allowing for multiple loci. This takes us back to the drawbacks of picking a single locus/gene, viz researchers focus on a single gene thus losing information from all other loci. Solution: Our methodology doesn’t collapse any loci, allowing for maximum use of all information.
Another type of analysis seeks to find the percentage of the population that has an effect via a certain locus. For example, Barrett [2] says that “Assuming an autosomal recessive model we estimate that approximately 35% of families in our data set are linked to this locus.” Thus, across the different types of studies that are currently performed or have been performed, the underlying goal is to seek a single gene (or multiple unconnected genes). However as we have described above, there is no reason that a single gene is the sole determinant of a complex disease. Solution: Although this could be one type of unification of the results, it really recapitulates the drawback of earlier results, which is that they try to imagine one locus and therefore one gene as their focus. Our ranked list is one way to unify the results, but as shown next it is not enough.
Given that a complex disorder such as autism is multigenic, why is it not enough to simply list all the ranked genes? Why is it necessary to further unify the results? Any disorder has some mechanism, and the goal is to identify it. Although there is considerable clinical heterogeneity in autism, there is concordance [20] amongst specialists with respect to symptoms in affected children. Therefore, even if autism has complex etiologies, it has an underlying molecular physiology overlap shared by autistics. This overlap may occur at several levels (ranging from clinical symptoms to gene expression). Because biological pathways reflect mechanisms underlying biological function, one design criteria for a new method is to find such overlap across pedigrees. In essence therefore, each pedigree may contribute in some way to a unified mechanism in autism. Just as genes closer to loci are more linked to a disorder, the same is true of pathways. In addition, an analysis that combines genes into pathways also affords us the opportunity to increase the signal, given by a factor of m0.5 where m is the number of genes in the pathway [21]. Our signal strength now is given by the score for each pathway. By also searching for pathways, we contexualize our results giving us a better measure of the importance of any gene proximal to a locus. One of the main drawbacks in current approaches is that there is no unification across the several loci implicated [22], and our approach presents a solution. Also, from 5d above, we note that simply doing an enrichment on the closest genes will also not be optimal since we are not sure where the true signal lies and because of the other reasons presented above.
Above, we have shown the rationale behind LoGS and its derivation of LoGS. The methods section describes in detail the execution of LoGS. We present next the bias testing that was conducted.
Testing the results of LoGS
We tested if the results of LoGS finding immune function themes in autism are methodology-dependent (i.e. could our methodology show immune themes because of immune genes collecting with microsatellites compared with all other genes). We thus looked for immune enrichment next to both our autism loci and to randomly drawn microsatellites. Further, we ran LoGS on two other diseases to see if the same pathways show up at the top. We present these analyses below.
Microsatellites in general are not immune enriched: Two analyses for g-d were run on immune genes (methods): i. 29 autism loci. ii. Microsatellite sampling (1000 runs). These analyses were repeated for 8 additional gene sets. The 29 autism loci showed a g-d of -0.0004 (RDa(Mb), (Table 1). Thus, regardless of what may happen at the microsatellite level in general, immune genes aren’t enriched next to autism loci (this is also borne out when we look for enrichment of all genes within 50cM of all autism loci). The immune theme microsatellites analysis showed that the average of 1000 permutations had an enrichment of 0.0089 (RDm, Table 1). However, the whole genome analysis shows an enrichment of 0.012. This shows that genes on average in the genome are slightly enriched next to microsatellites in general and comparatively immune genes are slightly less enriched. Further, all other gene sets or pathways tested showed a higher g-d difference than either the genome or autism. These results taken together show that immune function genes are not enriched next to microsatellites in general and are de-enriched next to our autism loci (even when we look at the RDa(cM) which is positive, and this is because in general 1cM does not equal 1Mb, we note that this number is still less positive than the whole genome RDm number). Our results therefore are not emanating from any bias in the distribution of immune genes next to microsatellites (Table 1).
| Pathway | N | RDm | RDa(Mb) | RDa(cM) | Pm | P |
|---|---|---|---|---|---|---|
| Immune | 1491 | 0.0089 | -0.0004 | 0.0119 | 0.419 | 5.10-1 |
| Synapse | 428 | 0.0172 | -0.0087 | -0.0121 | 0.287 | 1.10-4 |
| Angiogenesis | 299 | 0.0140 | 0.0092 | 0.0141 | 0.436 | 2.10-2 |
| Cell cycle | 1236 | 0.0107 | -0.0047 | -0.0062 | 0.319 | 7.10-1 |
| Growth | 682 | 0.0219 | 0.0001 | 0.0141 | 0.274 | 1.10-12 |
| Pigmentation | 76 | 0.0062 | -0.0012 | 0.0334 | 0.439 | 8.10-2 |
| Cell death | 1505 | 0.0121 | -0.0076 | -0.0100 | 0.280 | 2.10-1 |
| Cell respiration | 131 | 0.0140 | -0.0634 | -0.0552 | 0.097 | 7.10-2 |
| Genome | 21147 | 0.0101 | 0.0041 | 0.0024 | 0.427 | 1 |
Table 1: Testing for clustering of genes next to microsatellites. RD = ratio difference, g-d. P = P value based on t test comparing each pathway with the genome (with 1000 Marshfield marker random samplings for each). RDm = average RD using Marshfield markers within 50Mb of each random locus. RDa(Mb) = RD within 50Mb of all autism loci. RDa(cM) = RD within 50cM converted to Mb. Pm = Permutation P value of autism loci versus Marshfield distribution. N = total number of genes in the pathway.
Other diseases do not necessarily implicate the same pathways: We also wanted to compare the results of LoGS (immune pathways derived from CNVs in autism iCNV-a through e) with other diseases where immune function is very likely and known to play a role. While it may be possible for other diseases to be enriched for the very same pathways we found in autism, if these pathways were to be top ranked in all other diseases studied without exception, then that could show some bias in our methodology. We thus tested LoGS in multiple sclerosis and systemic lupus erythematosus. In MS, all five pathways were below rank 79 while in lupus iCNV-a, iCNV-b, iCNV-c, and iCNV-e was not even found within 50cM of the lupus loci and iCNV-d although present was ranked 25. Thus, these pathways do not always obtain top ranks in other diseases (Table 2).
| pathway | MS rank | SLE rank |
| i-CNV-a | 94 | NA |
| i-CNV-b | 79 | NA |
| i-CNV-c | 101 | NA |
| i-CNV-d | 103 | 25 |
| i-CNV-e | 80 | NA |
| i-CNV-a | 94 | NA |
Table 2: iCNV-5 are not top ranked in either Systemic Lupus Erythematosus (SLE) or Multiple Sclerosis (MS). Most of the iCNV-5 genes are not even present in the 50cM windows of the SLE dataset.
1_ifn_alpha_beta (i-CNV-a)
2_hematopoietin_ifn_class (i-CNV-b)
4_response_to_virus (i-CNV-c)
5_antiviral_response_protein_activity (i-CNV-d)
3_cytokine_activity (i-CNV-e)
This test is a very limited test only looking for a very small sampling of immune pathways that are relevant in autism and does not purport to test all immune genes in these diseases. We are simply testing whether the results of LoGS in autism are deriving from some bias in the distribution of those pathways and not whether immune function itself is important in SLE or MS.
EASE enrichment of all genes within 50cM of autism loci: EASE was run over all genes within 50cM of the 29 autism loci (Table 3) [23]. Not only is immune function not found in the top 20, but the highest rank with immune function occurs at rank 110--inflammatory response. This is also seen above where immune function genes aren’t enriched within 50Mb of the autism loci (g-d analysis above). This is a strong validation for running a LoGS analysis because it picks up the most important pathways closest to the markers taken together. An enrichment for all genes fails to find such signals.
LoGS form an important new method that can help ascertain genetic mechanisms underlying complex disorders. Furthermore since it works directly at the genomic level it gives us a direct measure of the mechanism that might be responsible in the disease without regard to tissue expression as well as environmental influences (epigenetic influences modify however the story derived from the genomic level).
In our prior study of autism, using two different genome analyses, LoGS and CNV, we found immune and developmental pathways. In this study, we addressed the important question of whether there is an underlying bias in the distribution of the underlying loci that are used in implementing LoGS. We show through several mechanisms that there in fact isn’t any such bias.
It is also important for us to describe in some detail the rationale behind the construction of LoGS. Folkersen points to “the necessity of careful studies of genetic marker data as a first step toward application of genome-wide association studies findings in a clinical setting.” [4] LoGS presents our solution to problems inherent in current non pathway-based methods. In a nutshell, pathway analysis strengthens the signal emanating around a locus. It is unlikely for several genes that function together to be proximal together across the loci of interest by chance versus for a single gene to be proximal by chance. Also, another conceptual way to look at this is the following. Say we have an implicated locus in autism. Say also that this locus sits either within or proximal to a gene that is quite large (say dystrophin which is 2.4 million bases long). Because this gene spans such a large area a locus close to it is more likely to point to this gene (in the extreme case, if a gene were to be 100cM centered on the locus, there would be no ambiguity about which gene proximal to the marker is the correct gene). Pathway analysis is akin to ‘increasing’ the size of a gene by bringing in other genes from a common pathway. Our results show that immune function may play a critical role in the genesis, development, or manifestation of autism in the context of 5 pathways that we described earlier [1] and that were constructed from a CNV analysis in autism.
We used the Hapmap database to derive genetic distances in the following sections where genetic distances are described or used.
Linkage ordered Gene Sets (LoGS) (Figure 1)
Figure 1: Conceptual view of LoGS. A. Line up loci from all chromosomes (genes from each chromosome are shown with a different color for clarity). B. Collapse all loci to one point and project all genes next to this point. C. Take absolute values of gene distances. D. Remove color coding. Expand the area for clarity. E. Hypothetical pathways P1 and P2 and their memberships. F. Compute score V for P1 and P2.
The introduction outlines LoGS’ rationale and development. Here we present its details:
Compile pathways or gene sets to be used in LoGS as previously described [21]: A gene set is a set of genes that work together because they are in the same pathway or show relevance to each other. We searched various databases for such gene sets for eg. Gene Ontology (geneontology.org) and KEGG (genome.jp/kegg)--and added previously compiled genesets [21]. We also generated gene sets from publications where groups of genes were shown having some relevance to a process. The five pathways generated from the CNV analysis were also added.
Find all loci in the genome relevant to autism: We searched the literature for all autism loci which showed a LOD score above 3, looking at Online Mendelian Inheritance in Man (OMIM), pubmed, google scholar, and google. Most were microsatellites and a few were SNPs (Table S8 in (1)). Microsatellites span a region of the genome while SNPs are point locations. Twenty nine genetic loci along with their physical distances in the genome were obtained (Table S8 in (1)). For Loci with more than one LOD score (entries 20, 21), the lower score was used to be conservative. We converted physical distances to genetic distances (because they are more relevant to linkage) via the hapmap dataset (hapmap.org) containing a dense map of all genomic SNPs and their physical and genetic distances. To find the genetic distance for a microsatellite, we took the average of its start and end physical distances and looked for the closest SNP in physical distance units from hapmap. The microsatellite was then assigned the genetic distance of that closest hapmap SNP. For the SNPs in the dataset, we used the same procedure without running any average because SNPs are point locations.
Obtain a database of all human genes: Using the ensembl database, we obtained a list of all genes with their physical distances. Each gene’s location range was converted into a genetic distance in the following way. We looked for all SNPs within a gene’s start and end physical distances. When a gene had more than two SNPs within it, we took the SNPs closest to the two ends and averaged their genetic distances via hapmap. The gene was then assigned this average. Those genes that did not contain a SNP were not used. Because different sources can have different genetic distances for the same marker or gene, we used ensembl to find the locations of microsatellite markers and genes and then consistently used hapmap to convert such physical distances to genetic distances.
Rank genes: We found windows of 50cM on either side of each locus defined in step one by adding and subtracting 50cM to each locus (6905 genes were obtained via this step) and located all genes within these windows. When windows overlapped, genes in the overlap region were assigned to their closest locus. Because each gene is measured from its closest locus, we effectively placed all loci at some hypothetical origin (Figures 1A and 1B). Because we took our metric to be distance from a marker or locus, distances to the left of a marker were treated the same as distances to the right (Figure 1C). For each gene, the LOD score assigned to that gene was divided by its distance from the marker (we called this the signal metric‘s’. All genes were next ranked by‘s’.
Compute pathway ranks: Previously constructed gene sets were each given a score, V. To obtain this score, we ranked all genes in our system (using the signal metric ‘s’ ), and then assigned to each gene in the ranked list one of two numerical ratings (using the Kolmogorov- Smirnov statistic [21]).
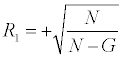 (when the gene is in the pathway),or
(when the gene is in the pathway),or
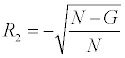 (when the gene is not in the pathway).
(when the gene is not in the pathway).
N is the total number of genes in the ranked list and G is the number of genes in the pathway for which we are computing V. Next, each gene in the ranking was given a value, C [21]. C for a gene equals the cumulative sum of the ratings (either of R1 or R2) of all genes above it (including itself). The highest C equals V for that pathway. Pathways are then ranked by their V scores. V for a pathway is thus obtained via the assignment of three numbers to each gene: signal metric s, rating R, value C.
Test top ranked pathway (immune function) for bias in its distribution in the genome
LoGS ranks certain immune function gene sets topmost in autism (these were derived from CNVs in autism). If immune function genes in the genome preferentially cluster around microsatellite markers from which the autism markers themselves are drawn, we would expect immune function genes to show up in a random sampling of markers. These results in autism could then show those particular immune function gene sets as a result of this clustering. We therefore ran two further analyses:
Random sampling of microsatellite markers to test for bias in immune function: We take the difference of two ratios: gene ratio, g (number of immune genes within 50Mb windows of a set of loci to all immune genes in the genome (from geneontology)) minus distance ratio, d (fraction of whole genome within 50Mb windows (whole genome size obtained from Hapmap)). Because of overlap between windows, d is in general not equal to number of loci times 100Mb. If the immune genes are evenly distributed across the genome, g-d for randomly chosen markers/locations on average will be zero.
We run 2 analyses:
i) A single g-d for 29 autism loci using immune genes. This will tell us if the immune function genes cluster preferentially within the 50Mb windows. To see if immune genes cluster next to microsatellites in general (from which autism markers are themselves drawn), we ran analysis ii.
ii) This analysis takes a standard microsatellite set (7) with 289 markers, adds microsatellites and SNPs in the autism dataset that weren’t in that set (bringing the total to 310), chooses 30 markers randomly and obtains g-d, repeats this 1000 times, and then obtains an average g-d. This g-d tells us if immune genes cluster with microsatellites. We compare these numbers with some background distribution to see if they are in fact immune-specific versus microsatellite specific. If microsatellites in general are gene enriched then they may also be immune enriched. To test this, we ran additional pathways. The whole genome pathway served as our background distribution, while the other 7 (Table 1) provide variability from it. To see this more clearly, consider the extreme case where all genes in the genome are within 50Mb of autism loci, giving an always positive g-d. However, no pathway will now show enrichment. This shows that variability is only meaningful w.r.t. the background genome distribution. We used Mb rather than cM, because genetic distance (in cM) does not cover the same length of the genome in Mb across the genome (Figure 2). However, on average we calculated 100cM = 100.5Mb.
Run LoGS on other diseases to look for immune function pathways at the top: Two additional diseases were analyzed via LoGS to see if they show the same pathways (iCNV-5) at the top.
Running EASE on all genes within 50 cM: As was done in the structural variations analysis, EASE was used to find the top pathways on all genes within 50cM of the autism loci.
Construction of the microsatellite marker set: In the bias testing above, we have used microsatellite markers. This section describes the construction of such sets in the analysis.
We obtained the complete set of all types of markers listed at ensembl (these include SNPs as well). We were not aiming for a comprehensive listing of markers, but rather for a number that is typically on the order of the numbers of markers used. We wanted to be conservative, because each study can only use a limited number of markers. Researchers typically use microsatellite sets on the order of 300-400 in linkage studies. This could be for reasons of practicality among others. For eg, Risch et al used 346 markers [7]. This paper also used a standard microsatellite set known as the Marshfield set. If we had picked all the 300,424 markers available at the ensembl database, then we would have simply scanned the whole genome and we wouldn’t be randomly drawing from some type of a representative set for any linkage study. And thus, we would not be able to find any bias if any that may exist.
Because our analysis uses the linkage peaks implicated in various analyses conducted previously by several researchers, we wanted to make sure that our sampling for random microsatellites was drawn from a set that was representative of those used by others in both the types of microsatellites used as well as their number. Further, we also wanted to make sure that those microsatellites that were not found in the standard Marshfield set but were part of our autism collected set were then added to our sampling set to give us a complete representation in our sampling set (we also added SNPs that were in our collected set but which would by definition not be in any microsatellite database). We also repeated the analyses without adding the left over markers in our dataset to the standard Marshfield set with no change in the patterns described.
The standard Marshfield set was obtained from the Marshfield database (https://research.marshfieldclinic.org/genetics/GeneticResearch/ screeningsets.asp). This database has 366 markers. We next filtered this set for those microsatellites that were also found at ensembl.org leaving us with 289 markers. To this we added all the SNPs in our data plus the microsatellites that were not in the Marshfield dataset so that our sampling would include our data. This brought the total to 310. We ran both analyses (with the 21 extra loci and without) and the results remained unchanged.
Computation of g-d in autism and g-d for random microsatellites
We want to test the idea whether immune function genes in general cluster next to microsatellites in general and further whether they might also cluster next to autism specific loci the 29 loci used. This is important because if there is preferential clustering or enrichment of immune genes next to all microsatellites, then when microsatellites are chosen for a study in autism, the significant loci identified in autism may derivatively show a bias. The results thus may not reflect any mechanism of such pathways in autism but rather this underlying sampling bias.
We worked with the following hypothesis. If genes in the genome are randomly and evenly distributed, then the fraction of genes within a certain region of the genome (g) should be equal to the fraction of the genome (in size) covered (d) and that their difference for a comprehensive immune pathway when compared with the difference for the genes in the whole genome can give us an idea of the enrichment or lack thereof of that the immune pathway. We obtained a listing of all genes for several pathways including immune function (geneontology. org) and also including a listing of all genes in the genome (ensembl. org). For each such pathway (including the whole genome), we looked for the numbers of genes within 50cM windows versus the total number and computed their ratio (g). We next found the fraction of distance occupied by the 50cM windows (d). For the analysis using microsatellites, we sampled 30 microsatellites randomly and compute g-d and repeated 1000 times, and then found the average.
Size variation in Mb across the genome for 100 cM
Based on the Hapmap data, we took 100cM differences across the genome randomly 1000 times and then for each 100 cM section of the genome, we obtained the physical distance in Mb (Figure 2). The average across these 1000 runs gave us close to the often cited figure of 100Mb in the literate (our average was 100.5 Mb).