Research - (2020) Volume 8, Issue 3
Based on the generated database of 413 sample plots with definitions of stand biomass of the genus Populus spp. in Eurasia, from France to Japan and southern China, statistically significant changes in the structure of forest stand biomass were found with shifts in winter temperatures and average annual precipitation. When analyzing the reaction of the structure of the biomass of the genus Populus to temperature and precipitation in their transcontinental gradients, the clearly expressed positive relationship of all components of the biomass with the temperature of January is visible. Their relationship with precipitation is less clear: in warm climate zones, when precipitation increases, the biomass of all wood components decreases intensively, and in cold climate zones, this decrease is less pronounced. The foliage biomass does not increase when precipitation decreases, as is typical for wood components, but decreases. This can be explained by the specifics of the functioning of the assimilation apparatus, namely, its transpiration activity, when warming and the corresponding increase in transpiration requires an increase in the influx of assimilates into the foliage, and the desiccation of the climate reduces this influx of assimilates. Perhaps this phenomenon demonstrates the future scenario of acclimatization of trees to the ongoing warming and changes in the water balance of territories. The results obtained can be useful in the management of biosphere functions of forests, which is important in the implementation of climate stabilization measures, as well as in the validation of the results of simulation experiments to assess the carbon-deposition capacity of forests.
Genus Populus spp.; Regression models; Stand biomass; Biomass structure; Climate change; Average January temperature; Average annual precipitation
Active human economic activity has led to significant global changes in the functioning of the biosphere, and the observed climate warming has a significant impact on the vegetation cover of the planet [1,2]. If earlier the problems of assessing climate impacts on vegetation had a regional character [3]. In recent decades it has become clear that the problem reaches a global, general planetary level and largely determines the future fate of human civilization [4,5]. Mapping the distribution of Net Primary Production (NPP) over the surface of the planet by extrapolating empirical NPP data obtained from forest sample plots to large areas of biomes or to latitude gradients does not allow making any predictions of changes in the climate-NPP system [6-9]. The same can be said about the common planetary patterns of distribution of NPP harvest data by gradients of average temperatures and precipitation [10].
Due to the species-specific responses of trees and stands to climate changes and the complexity of their morphological structure, changes in bio-productivity within biomes and continents are modeled using compiled databases of empirical data on individual tree species and taking into account their morphological structure. Techniques are used to harmonize models based on dummy variables that encode the regional affiliation of the harvest data [11,18]. It is known that changes in the vegetation cover of Eurasia occur both in the latitudinal direction due to changes in the PhAR, and in the meridional direction due to changes in the climate continentality [19,20]. Therefore, models of the biomass of trees and stands have been developed, including as independent variables their mass-forming indices, as well as indices of natural zoning and climate continentality [21-23].
Due to current climate changes, priority is given to changing the biomass and NPP of forest ecosystems under the influence of average temperatures and precipitation. Similar studies are performed at both a regional and transcontinental levels [13,15,24- 29]. Studies of forest stand biomass at the transcontinental level, performed for four coniferous species of Eurasia, showed that changes in their biomass due to temperatures and precipitation are species-specific, i.e. they differ between species both in the total and above ground biomass, and in the component composition.
It seems relevant to investigate similar patterns for hardwoods. This article is devoted to the study of transcontinental climate-related trends in the structure of forest biomass formed by fast-growing species of the genus Populus spp. Across the northern hemisphere, this genus plays a disproportionately important role in promoting biodiversity and sequestering carbon. It is illustrative of efforts to move beyond single-species conservation worldwide. Genus Populus is valued for many reasons, but one highlights their potential as key contributors to regional and global biodiversity [30]. A tremendous need in paper, cardboard and board materials open almost unlimited opportunities of this genus wood economic use. By density and cellulose content, poplar wood does not come up short to the coniferous species. Despite the slightly shorter wood fiber of poplar in comparison to spruce, modern technologies make the first class production of paper, cardboard and wood board materials out of this “disgraced” species possible. But today, the genus Populus is an example of a particularly evident disparity between the potential organic matter production in plantations and its actual implementation in the boreal natural forests [31].
To analyze geographical patterns of biomass distribution in Eurasian forests formed by stands of the genus Populus spp., from the author's database in the amount of 8 thousand sample plots, the materials of 413 determinations with the data of the biomass structure were used [32]. These biomass data are presented in different components (stems, branches, foliage, and roots). The distribution of sample plots with biomass data of the genus Populus spp. on the map-scheme of Eurasia is shown in Figure 1, and according to tree species and countries in Table 1.
| Species | Botanical title | Country | Plot Quantity |
|---|---|---|---|
| Quaking aspen | Populus tremula L. | Russia, Ukraine, Kazakhstan, Estonia, Belarus | 188 |
| David's aspen | P. DavidianaDode | China, Japan | 129 |
| Californian poplar | P. TrichocarpaTorr. and A.Gray ex Hook. | France, Austria, Belgium, Netherlands | 37 |
| Poplar larrity | P. laurifolia Ledeb. | Russia | 12 |
| White poplar | P. alba Ledeb. | Russia, Kazakhstan | 10 |
| Poplar «Robusta» | Populus × euroamericana | Ukraine | 10 |
| Asiatic poplar | P. euphratica Olivier | China | 9 |
| Hybrid | Populus hybrid | Japan | 8 |
| Poplar berry-bearing | P. Deltoides W.Bartram ex Humphry Marshall | China | 6 |
| Black poplar | P. nigra L. | Russia | 2 |
| Bahala poplar | Populus × bachelieri Solemacher | Bulgaria | 1 |
| Ploomy poplar | P. PruinosaSchrenk | Tajikistan | 1 |
| Total | 413 | ||
Table 1 : Distribution of plots with determinations of Populus biomass (t/ha) by species and countries.
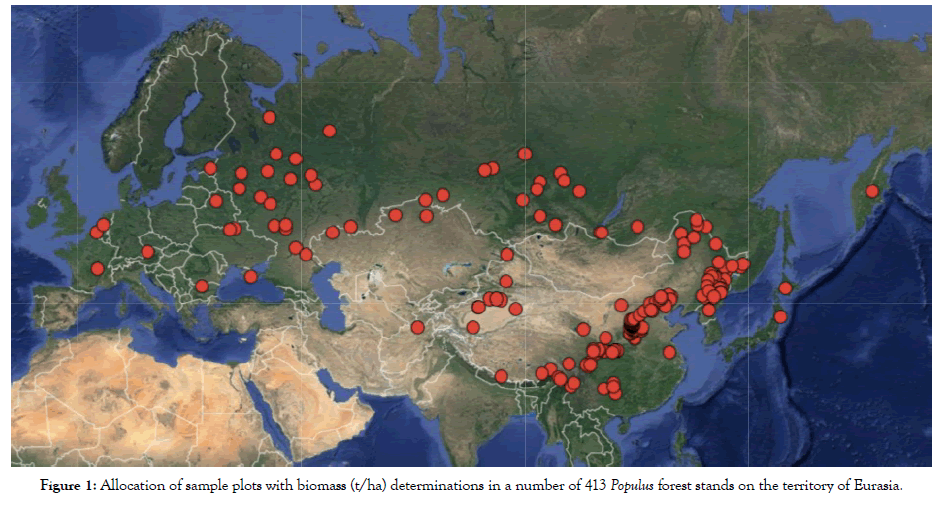
Figure 1: Allocation of sample plots with biomass (t/ha) determinations in a number of 413 Populus forest stands on the territory of Eurasia.
As plots for estimating biomass of forest stands are usually established in typical 'background' habitats, that are representative in relation to this type of plant communities, one can make on their basis a preliminary geographical analysis of biomass gradients of pine forests. For analytical description of geo-graphic distribution patterns of biomass productivity of forest cover, one must choose the geographical characteristics of the territory of Eurasia that can be expressed by the quantity and measure.
The actual values of the biomass of 413 stands of the genus Populus (Figure 1) based on the known coordinates of the sample plots established, we superimposed on the maps of winter (January) temperatures and average annual precipitation distribution and related them with the isolines of the mentioned indices on the maps [33]. In our case, the schematic map of the isolines of mean January temperature, rather than that of the mean annual temperature, was used, as climate warming is most pronounced in the cold half of the year [34,35]. Obviously, taking the mean winter temperature as one of the independent variables, we get a more reliable dependence having the higher predictive ability.
Then the compiled matrix of harvest data (Table 2) was subjected to the common regression analysis.
| A | N | V | Pi | Tm | PRm | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ps | Pb | Pf | Pa | Pr | Pt | |||||
| 40 | 0.790 | 208 | 89 | 5.5 | 2.40 | 98.0 | 21.6 | 119.6 | -7 | 570 |
| 21 | 0.278 | 218 | 99.8 | 20.7 | 4.19 | 129.7 | 29.2 | 158.9 | -3 | 570 |
| 12 | 12.54 | 62.5 | 34.8 | 4.45 | 1.91 | 41.2 | 15.0 | 56.2 | -13 | 290 |
| 22 | 4.550 | 30 | 16.1 | 4.24 | 0.80 | 21.1 | 6.0 | 27.1 | -13 | 290 |
| 49 | 0.650 | 284 | 113 | 22.5 | 3.07 | 138.6 | 57.0 | 195.6 | -20 | 317 |
| 41 | 0.526 | 192 | 76.0 | 22.2 | 2.40 | 100.6 | 55.0 | 155.6 | -18 | 250 |
| 78 | 0.518 | 200 | 88.83 | 28.37 | 4.99 | 127.7 | 38.79 | 166.5 | -15 | 570 |
| 45 | 0.500 | 105 | 49.62 | 10.92 | 4.52 | 67.56 | 8.58 | 76.14 | -26 | 570 |
| 78 | 0.666 | 185 | 103.1 | 45.44 | 8.75 | 163.9 | 37.8 | 201.7 | -15 | 570 |
| 27 | 2.935 | 142 | 84.29 | 17.56 | 7.01 | 114.0 | 42.73 | 156.7 | -9 | 820 |
| 68 | 1.244 | 223 | 102.4 | 22.44 | 7.43 | 138.5 | 51.47 | 190.0 | -15 | 570 |
| 25 | 4.066 | 122 | 73.51 | 11.31 | 5.89 | 95.04 | 36.6 | 131.6 | -15 | 570 |
| 40 | 1.062 | 224 | 99.81 | 32.82 | 7.69 | 146.6 | 45.47 | 192.1 | -15 | 570 |
| 34 | 1.595 | 182 | 95.77 | 13.15 | 7.91 | 122.6 | 52.18 | 174.8 | -10 | 444 |
| 50 | 1.510 | 163 | 75.11 | 22.44 | 6.21 | 108.4 | 34.26 | 142.7 | -25 | 444 |
| 28 | 7.32 | 129 | 73.0 | 11.40 | 2.00 | 89.93 | 17.2 | 107.1 | -15 | 570 |
| 37 | 2.913 | 153 | 86.65 | 18.56 | 6.27 | 116.7 | 41.79 | 158.5 | -15 | 570 |
| 69 | 0.811 | 284 | 110.9 | 17.20 | 7.62 | 142.2 | 56.36 | 198.6 | -26 | 444 |
| 58 | 1.188 | 124 | 61.47 | 16.79 | 3.66 | 85.63 | 27.24 | 112.9 | -26 | 444 |
| 79 | 0.403 | 163 | 68.75 | 18.91 | 3.66 | 95.43 | 29.6 | 125.0 | -26 | 444 |
| 38 | 4.255 | 121 | 73.56 | 11.79 | 6.19 | 95.95 | 38.21 | 134.2 | -15 | 570 |
| 68 | 1.822 | 234 | 117.3 | 30.29 | 7.23 | 162.0 | 54.8 | 216.8 | -26 | 444 |
| 29 | 2.000 | 61 | 34.42 | 16.31 | 2.77 | 55.88 | 16.57 | 72.45 | -5 | 826 |
| 39 | 2.774 | 62 | 37.92 | 8.72 | 3.00 | 58.27 | 9.41 | 67.68 | -5 | 826 |
А :Age (yrs); V: Stem Volume (m3/hа); N: Tree Density (1000/hа); i: Index of biomass component; t: Total wood storey; a: Aboveground wood storey; r: Underground wood storey or roots; s: Stem over the bark; f: Foliage; b: Branches; PRm: Mean annual precipitation (mm); Тm: Mean january temperature(°С).
Table 2 : A fragment of the original matrix of experimental data.
Basic principles of modeling and the results obtained by means of regression analysis should have ecologic-geographical interpretation. Biological productivity of forests is depending on climatic factors, but only as a first approximation, since there are ontogenetic, cenotic, edaphical, and other levels of its variability. Therefore, we include in the regression equations the independent variables explaining the variability of the dependent variable, expressing not only with climatic parameters but also with forest age, tree density and stem volume.
Because mean January temperature in northern part of Eurasia has negative values, corresponding independent variable is modified to the form (Tm+50). Then the technique of multiple regression analysis (http://www.statgraphics.com/for more information) according to three blocks of recursive equations is used: two blocks of mass-forming indices N and V and single block of biomass Pi(arrows show the sequence of calculations)
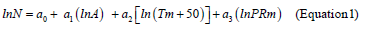
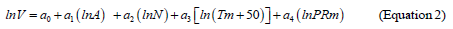
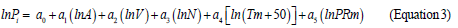
Results of calculation of equations 1-3 are listed in the Table 3. Only the variables that are significant at the level of probability of P95 and above are showed in this table. The equations are tabulated in the sequence illustrated by arrows. The results of tabulating the models in the sequence of equations (1), (2), and (3) present the rather cumbersome table. We took from it the values of the component composition of biomass of Populus forests for the age of 50 years and built 3D-graphs of their dependence upon temperature and precipitation (Figure 2).
| Dependent variables | Coefficients and independent variables | adjR2** | SE*** | |||||
|---|---|---|---|---|---|---|---|---|
| а0* | a1(lnA) | a2(lnV) | а3(lnN) | a5[ln(Tm+50)] | a6(lnPRm) | |||
| ln(N) | 10.7307 | -1.2994 | - | - | -2.4045 | 0.4747 | 0.623 | 0.74 |
| ln(V) | 5.9573 | 0.3617 | - | -0.2589 | 0.5288 | -0.6169 | 0.534 | 0.47 |
| ln(Ps) | -1.8923 | 0.2068 | 0.9123 | 0.0646 | 0.0764 | 0.0811 | 0.963 | 0.17 |
| ln(Pb) | -2.8796 | 0.2421 | 0.552 | -0.0537 | 0.3792 | 0.0678 | 0.675 | 0.44 |
| ln(Pf) | -4.0545 | 0.007 | 0.4127 | 0.1332 | -0.0589 | 0.5272 | 0.522 | 0.38 |
| ln(Pr) | -3.5174 | 0.0497 | 0.7113 | 0.0563 | 0.2306 | 0.3533 | 0.72 | 0.35 |
| ln(Pa) | -1.2511 | 0.1782 | 0.8183 | 0.0463 | 0.0984 | 0.096 | 0.955 | 0.17 |
| ln(Pt) | -1.1022 | 0.0477 | 0.7969 | 0.0486 | 0.1467 | 0.1849 | 0.918 | 0.18 |
*The constant corrected for logarithmic retransformation by: Baskerville, 1972; **adjR2 : Determination coefficient adjusted for the number of variables;*** SE: Standard Error of the equations.
Table 3 : Characteristics of biomass equations 1-3.
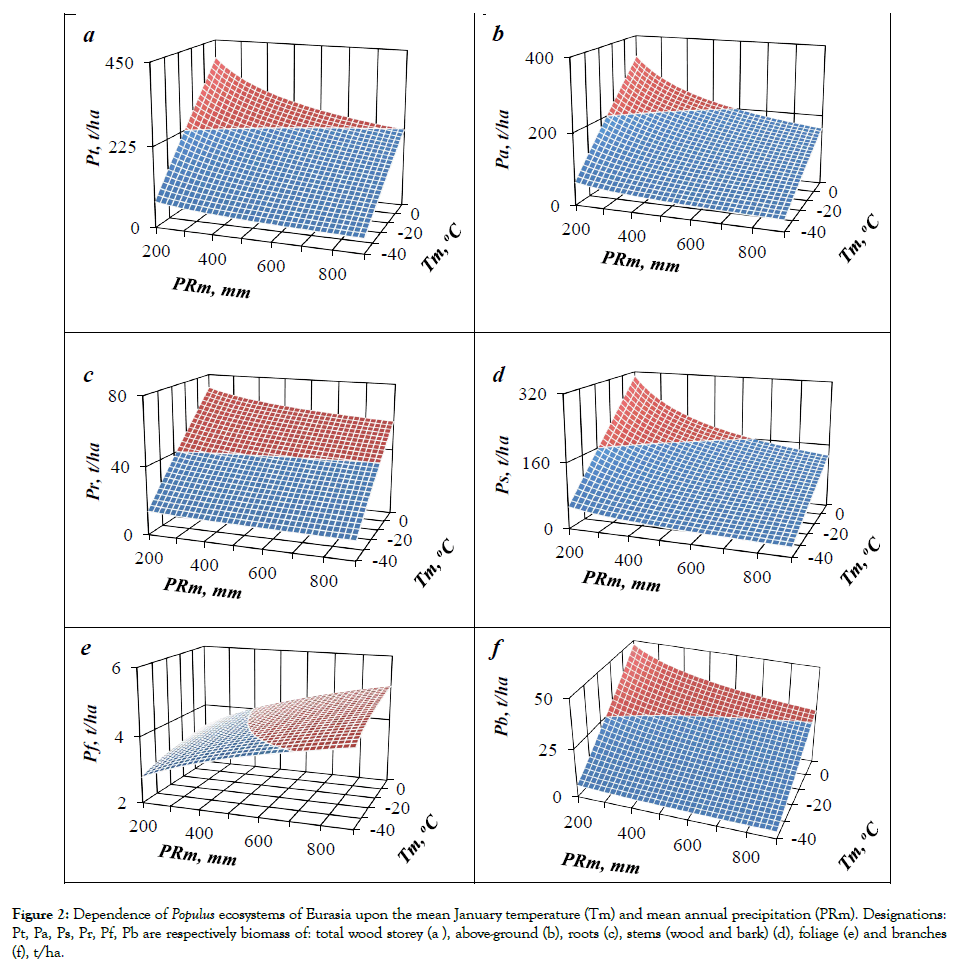
Figure 2 : Dependence of Populus ecosystems of Eurasia upon the mean January temperature (Tm) and mean annual precipitation (PRm). Designations: Pt, Pa, Ps, Pr, Pf, Pb are respectively biomass of: total wood storey (a ), above-ground (b), roots (c), stems (wood and bark) (d), foliage (e) and branches (f), t/ha.
When analyzing the reaction of the biomass structure of the genus Populus to temperature and precipitation in their transcontinental gradients, a clearly expressed unambiguous positive relationship of all components of the biomass with the average temperature of January is seen. Their relationship with precipitation is less clear: in warm climate zones (Tm=0°C), when precipitation increases, the biomass of all wood components decreases most intensively, and in cold climate zones (Tm=-40°C), this decrease is expressed to a much lesser extent.
At the first glance, it seems paradoxical reaction of the foliage biomass with increasing precipitation, which does not decrease, as is typical for wood components, but increases. This is consistent with a similar situation observed in Russian Siberia with respect to forest cover, where with a warming climate and a simultaneous decrease in precipitation, the share of assimilation mass decreases, and the share of wood components increases [36]. This is explained by the specifics of foliage functioning, namely, its transpiration activity, when warming and a corresponding increase in transpiration requires an increase in the influx of assimilates into the foliage, and the desiccation of the climate reduces this influx of assimilates due to a decrease in transpiration activity. Perhaps this phenomenon demonstrates the future scenario of acclimatization of trees to the ongoing warming and changes in the water balance of territories.
Based on a database of 413 sample plot with definitions of forest biomass of the genus Populus spp. of Eurasia in the territory from France to the South of China and Japan, a statistically significant increase in stem, above-ground and underground biomass was found with an increase in winter temperatures and a decrease in precipitation, especially in warm climate regions. In contrast to the woody components of biomass, the mass of foliage, increasing with warming, simultaneously decreases with a decrease in precipitation, which is due to the specifics of the functioning of foliage, namely, its transpiration activity.
The results obtained can be useful in the management of biosphere functions of forests, which is important in the implementation of climate stabilization measures, as well as in the validation of the results of simulation experiments to assess the carbon-deposition capacity of forests. They also provide a preliminary idea of possible shifts in forest biological productivity indicators under the influence of climate change.
Citation: Usoltsev VA, Shobairi SOR, Tsepordey IS, Chasovskikh VP(2020) Augmentative Modeling: A Pattern for Populus spp. Stand Biomass in the Eurasia under the Influence of Climate Change. J Climatol Weather Forecast 8:259.doi: 10.35248/2332-2594.2020.8.259
Received: 10-Jun-2020 Published: 31-Jul-2020, DOI: 10.35248/2332-2594.2020.8.259
Copyright: © 2020 Shobairi SOR, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.