Journal of Diabetes & Metabolism

Associations between body mass index and breast cancer markers

Author info »

Introduction

BMI has been a fundamental psychosocial issue among human beings for millennia. It is a composite measure of height and weight, which is defined as BMI= Weight(kg) / Height(m²). An individual fatness index is measured by BMI. It is considered as the risk factor for the growth of many diseases such as breast cancer, diabetes, cardiovascular diseases, etc. [1-5]. In general, BMI less than or equal to 25 kg/m² is treated as the normal, otherwise it is considered as obesity.

Excess weight has been associated with a variety of cancers such as postmenopausal breast, colon, renal, esophageal, endometrial etc. The International Research Agency on Cancer has predicted that BMI causes 9% of breast cancer, 25% of renal cancer, 11% of colon cancer, 39% of endometrial cancer, and 37% of esophageal cancer [6]. Calle et al. [7] pointed that BMI was associated with a greater risk of death from 14 cancers such as esophagus, liver, colon and rectum, gallbladder, kidney, pancreas, non-Hodgkin lymphoma, stomach, multiple myeloma, breast, prostate, cervix, uterus, and ovary, and it was predicted that BMI may account for 20% of all cancer deaths in women and 14% in men [7].

BMI is a well-known risk factor for postmenopausal breast cancer, whereas debatable outcomes have been presented in premenopausal women [8-10]. A large sample meta-analysis reported an inverse association between BMI and the chance of premenopausal breast cancer [11]. Recently, two large prevention data studies have shown that premenopausal women with higher BMI are at increased risk for growing breast cancer [12,13].

The associations between BMI and breast cancer are still contradictable [8,9,11,14-16]. These can be studied based on statistical modeling of BMI on the breast cancer biomarkers such as leptin, resistin, adiponectin and MCP-1, along with other explanatory variables. On the other hand, each breast cancer biomarker should be modeled on BMI along with other explanatory variables. The current report focuses the associations between BMI and breast cancer biomarkers based on modeling of BMI, MCP- 1, adiponection, resistin, and leptin. For a data set given in [17, 18], these models have been studied in [19-23]. From these models, the associations between BMI and breast cancer biomarkers are reported in the current article.

Materials and Methods

Materials

The data set is available in the UCI Machine Learning Repository, and its detailed description is given in [17, 18]. For immediate using of the covariates in the report, these are restated as BMI (kg/m²), Age, HOMA-IR, Insulin (μU/mL), Glucose (mg/dL), Adiponectin (μg/mL), Resistin (ng/mL), MCP-1, Leptin(ng/mL), Types of Patient (TYOP) (1=healthy controls; 2=patients).

Statistical methods

The considered data set given in [17, 18] is a multivariate data set. The interested responses are BMI, resistin, MCP-1, adiponectin, leptin which are all positive continuous heterogeneous and non-normally distributed. These are required to be modeled herein. These can be appropriately modeled using joint generalized linear models (JGLMs) adopting both the Log-normal and Gamma distributions, which are clearly given in [24-26]. Both the JGLMs under the Log-normal and Gamma distributions are very shortly given in recent articles [22-23], which are not reproduced herein. For more discussions on JGLMs, readers can visit [24, 25].

Statistical and graphical analysis

For ready reference, first we examine BMI model on age, insulin, glucose, and breast cancer biomarkers. The detailed analysis is given by Das et al. [19]. It is mentioned herein that BMI and breast cancer biomarkers such as MCP-1, resistin, leptin and adiponectin can be modeled adopting JGLMs under both the Log-normal & Gamma distributions [24-26]. Log-normal JGLMs fit of BMI is better than the Gamma fit, which is presented in Table 1, and its fitting diagnostic is revealed in Figure 1. Figure 1 displays the absolute residuals plot against the predicted BMI values, which is closely a flat straight line, implying that variance is constant with the running means. Figure 2 represents the normal probability plot of the fitted BMI mean Log-normal model in Table 1. No lack of fit is identified in both the figures. So, Log-normal fitted BMI model is an approximate form of its true model. Fitted BMI mean & dispersion models are as follows (Table 1).

Table 1: Results for mean and dispersion models for BMI from Log-Normal and Gamma fit.

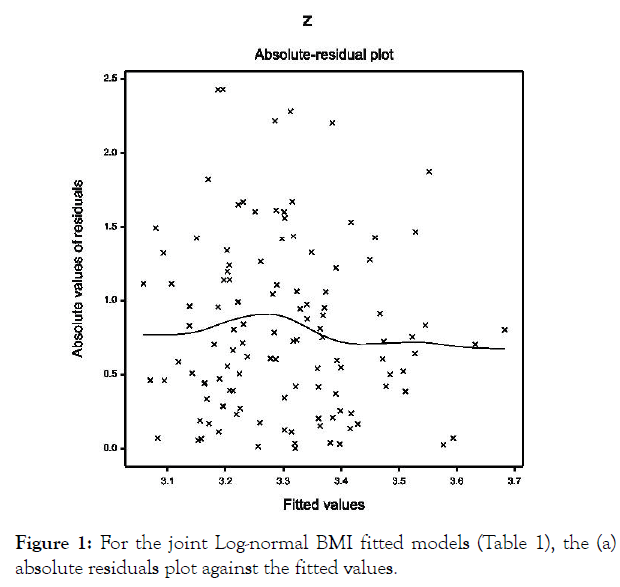
Figure 1: For the joint Log-normal BMI fitted models (Table 1), the (a) absolute residuals plot against the fitted values.

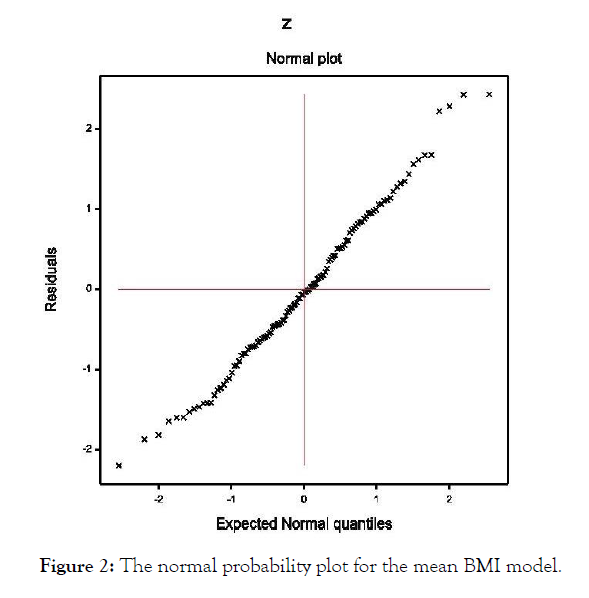
Figure 2: The normal probability plot for the mean BMI model.

Fitted Log-normal BMI mean (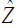) model (from Table 1) is 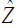= Log(BMI)= 3.0370 – 0.0421 HOMA-IR + 0.0015 Glucose + 0.0123 Insulin - 0.0068 Adiponectin + 0.0001 MCP-1 + 0.0053 Leptin – 0.0708 TYOP, and the BMI fitted Log-normal variance ( 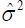) model is 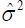= exp. (-4.445 - 0.018 Insulin – 0.019 Resistin + 0.015Age).

Breast cancer biomarker MCP-1 analysis is given by Kim et al. [20], and for ready reference it is reproduced in Table 2. Fitted MCP-1 mean & dispersion models are as follows.

MCP-1Gamma fitted mean (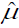 ) model (from Table 2) is 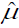= exp(5.1791 – 0.0265 Insulin + 0.0455 BMI – 0.0192 Leptin + 0.0220 Resistin + 0.0009 Insulin*Leptin ), and MCP-1Gamma fitted dispersion ( 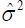) model (from Table 2) is 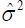= exp(0.7374 – 0.0868 Insulin – 0.0293 Age + 0.0051 Age*Insulin + 0.0053 Glucose – 0.8286 HOMA-IR – 0.0997 Leptin – 0.0405 Resistin + 0.0007 Glucose*Leptin + 0.0010 Leptin*Resistin) (Table 2).

Table 2: Results for mean & dispersion models for MCP-1 from Log-Normal and Gamma fit.

Breast cancer biomarker adiponectin analysis is given by Das and Lee [21], and for ready reference it is reproduced in Table 3. Fitted adiponectin mean & dispersion models are as follows.

Table 3: Results for mean and dispersion models for Adiponectin from Log-Normal and Gamma fit.

Adiponectin Gamma fitted mean (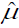) model (from Table 3) is 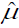= exp( 6.7778 - 0.1475 BMI - 0.0617 Age + 0.0020 Age*BMI - 0.0662 Resistin + 0.0282 Leptin + 0.0018 BMI*Resistin – 0.0008 BMI*Leptin), and Adiponectin Gamma fitted variance ( 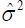) model (from Table 3) is 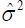= exp(-2.318 + 0.017Age). Breast cancer biomarker resistin analysis is given by Das and Lee [22], and for ready reference it is reproduced in Table 4. Fitted resistin mean & dispersion models are as follows.

Table 4: Results for mean & dispersion models for Resistin from Log-Normal and Gamma fit.

Resistin Gamma fitted mean (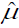 ) model (from Table 4) is 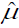= exp( 1.6651 – 0.0306 Leptin - 0.0052 Age + 0.0888 Adiponectin + 0.5421 TYOP – 0.1087 HOMA-IR+ 0.0007 MCP-1 + 0.0015 Age*HOMAIR - 0.0028 BMI + 0.0068 Glucose + 0.0014 BMI*Leptin - 0.0010 Glucose*Adiponectin - 0.0009 Leptin*Adiponectin), and Resistin Gamma fitted variance (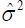) model (from Table 4) is 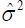= exp(- 4.8464 + 0.7971 TYOP + 0.1090 BMI + 0.0129 Leptin + 0.1885 Adiponectin – 0.0083 BMI*Adiponectin).

Breast cancer biomarker leptin analysis is given by Das and Lee [23], and for ready reference it is reproduced in Table 5. Fitted leptin mean & dispersion models are as follows.

Table 5: Associations of leptin with BMI, diabetes, age and breast cancer biomarkers.

Leptin Gamma fitted mean (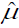) model (from Table 5) is 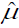= exp( -0.227 + 0.092 BMI + 0.006 Glucose + 0.010 Insulin + 0.025 Adiponectin + 0.016 Resistin – 0.001 MCP.1 – 0.001 Adiponectin*Resistin), and Leptin Gamma fitted variance (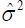) model (from Table 5) is 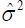= exp(-3.809 + 0.042 Age + 0.153 Resistin – 0.003 Age*Resistin).

Results

In Table 1, it is shown that mean BMI is positively associated with leptin (P<0.0001) and MCP-1 (P=0.0002), while it is negatively associated with adiponectin (P=0.0003), HOMA-IR (P<0.0001), and it is higher for healthy women (P=0.0116) than breast cancer women. In addition, variance of BMI is negatively associated with resistin (P=0.1450). On the other hand, from Table 2, mean MCP- 1 is positively associated with BMI (P<0.0001). In Table 3, it is shown that mean adiponectin is negatively associated with BMI (P<0.0001), BMI*Leptin (P=0.1729), while it is positively associated with Age*BMI (P=0.0017) and BMI*Resistin (P=0.0615). From Table 4, it is noted that mean resistin is positively associated with BMI*Leptin (P=0.0415), while its variance is positively associated with BMI (P=0.0942), and it is negatively associated with BMI*Adiponectin (P=0.1518). In Table 5, it is shown that mean leptin is positively associated with BMI (P<0.0001).

Discussion

The summarized analyses of BMI, MCP-1, adiponection, resistin and lepin are given in Tables 1-5. From Table 1, mean BMI is directly associated with leptin (P<0.0001), or MCP-1 (P=0.0002), concluding that it increases as leptin, or MCP-1 rises. In addition, it is inversely associated with adiponectin (P=0.0003), or HOMA-IR (P<0.0001), interpreting that it increases as adiponectin, or HOMA-IR decreases. Mean BMI is inversely associated with patient types (1=healthy women; 2= breast cancer patients) (P=0.0116), indicating that BMI is higher for healthy women than breast cancer women. Variance of BMI is partially inversely associated with resistin (P=0.1450), interpreting that BMI variance rises as resistin level decreases. Note that in epidemiology, partially significant effect is treated as confounder.

From Table 2, it is observed that MCP-1 is directly associated with BMI (P<0.0001), indicating that it increases as BMI increases. This is also observed from the BMI model as stated above. From Table 3, it is noted that mean adiponectin is inversely associated with BMI (P<0.0001), indicating that it decreases as BMI rises. This is also observed from BMI model. Mean adiponectin is directly associated with BMI*Resistin (P=0.0615), concluding that it rises as the interaction effect BMI*Resistin increases. In addition, mean adiponectin is inversely associated with BMI*Leptin (P=0.1729), indicating that it decreases as BMI*Leptin rises. Moreover, mean adiponectin is directly associated with Age*BMI (P=0.0017), concluding that it rises as the interaction effect Age*BMI increases. This implies that overweight women at older ages have higher level of adiponectin. From Table 4, mean resistin is directly associated with the interaction effect of BMI*Leptin (P=0.0415), concluding that it rises as interaction effect of BMI*Leptin increases. Variance of resistin is directly associated with BMI (P=0.0942), interpreting that it increases as BMI increases. Variance of resistin is inversely associated with BMI*Adiponectin (P=0.1518), indicating that it rises as BMI*Adiponectin decreases. From Table 5, mean leptin is directly associated with BMI (P<0.0001), indicating that it rises as BMI rises. This is also observed in BMI model. All the above summarized associations between BMI and breast cancer biomarkers are displayed in Table 6.

Table 6: Associations between BMI & breast cancer biomarkers.

The present derived associations between BMI and breast cancer biomarkers are little compared with the previous findings as the earlier research articles have not considered all these BC biomarkers along with BMI. In addition, the earlier articles have not considered probabilistic joint modeling to derive these associations. All these reported results herein are only based on the articles [19-23].

Conclusions

The report examines the associations between BMI and breast cancer biomarkers such as MCP-1, leptin, adiponection and resistin. These associations are reported herein considering the models of BMI and each breast cancer biomarkers. From these models, it can be concluded that BMI and breast cancer biomarkers are associated in both mean and variance models. BMI increases as leptin, or MCP-1 increases, or adiponection, or resistin, or HOMAIR decreases. Many interaction effects such as BMI*Leptin and BMI*Adiponectin are associated with resistin, while BMI*Resistin, BMI*Leptin and Age*BMI are associated with adiponectin. The report gives clear associations between BMI and breast cancer biomarkers which are very helpful to the researchers and medical practitioners. Medical practitioners and women should care on BMI along with breast cancer biomarkers.

Conflict of interest: The authors confirm that this article content has no conflict of interest.

References

1. Williams CL, Hayman LL, Daniels SR, Robinson TN, Steinberger J, et al. Cardiovascular health in childhood: A statement for health professionals from the Committee on Atherosclerosis, Hypertension, and Obesity in the Young (AHOY) of the Council on Cardiovascular Disease in the Young, American Heart Association. Circulation 2002;106:143-160.
2. US Dept Health and Human Services. The Surgeon General’s Call to Action to Prevent and Decrease Overweight and Obesity. Rockville, MD: US Department of Health and Human Services, Public Health Service, Office of the Surgeon General 2001
3. National Institutes of Health. Clinical guidelines on the identification, evaluation, and treatment of overweight and obesity in adults-the evidence report.  Obes Res. 1998; 6:51-209.
4. Gunter MJ, Xie X, Xue X, Kabat GC, Thomas ER, Wassertheil-Smoller S, et al. Breast Cancer Risk in Metabolically Healthy but Overweight Postmenopausal Women. Cancer Res. 2015; 75:270-274.
5. Key TJ, Appleby PN, Reeves GK, Roddam A, Dorgan JF, Longcope C, et al. Body mass index, serum sex hormones, and breast cancer risk in postmenopausal women. J Natl Cancer Inst. 2003; 95:1218-1226.
6. Harri Vainio, Rudolf Kaaks, Franca Bianchini Weight. Control and physical activity in cancer prevention: international evaluation of the evidence. Eur J Cancer Prev. 2002; 11:S94-100.
7. Calle EE, Rodriguez C, Walker-Thurmond K, Thun MJ. Overweight, obesity, and mortality from cancer in a prospectively studied cohort of U.S. adults. N Engl J Med.  2003; 348:1625-1638.
8. Van Den Brandt PA, Spiegelman D, Yaun SS, Adami HO, Beeson L, Folsom AR, et al. Pooled analysis of prospective cohort studies on height, weight, and breastcancer risk. Am J Epidemiol. 2000;152:514-527.
9. Morimoto LM, White E, Chen Z, Chlebowski RT, Hays J, Kuller L, et al. Obesity, body size, and risk of postmenopausal breast cancer: The Women’s Health Initiative (United States). Cancer Causes Control 2002; 13:741-751.
10. Lahmann PH, Hoffmann K, Allen N, H-van GC, Khaw KT, Tehard B, et al. Body size and breast cancer risk: findings from the European Prospective Investigation into Cancer and nutrition (EPIC). Int J Cancer. 2004;111:762–771.
11. Renehan AG, Tyson M, Egger M, Heller RF, Zwahlen M. Bodymass index and incidence of cancer: a systematic review and meta-analysis of prospective observational studies. Lancet. 2008; 371:569-578.
12. Cecchini RS, Costantino JP, Cauley JA, Walter MC, Lawrence WD, Stephanie RL, et al. Body mass index and the risk for developing invasive breast cancer among high risk women in Nsabp P-1 and Star Breast Cancer Prevention Trials. Cancer Prev Res (Phila). 2012; 5:583-592.
13. Macis D, Guerrieri-Gonzaga A, Gandini S. Circulating adiponectin and breast cancer risk: a systematic review and meta-analysis.  Int J Epidemiol. 2014; 1226-1236.
14. Dumitrescu RG, Cotarla I. Understanding breast cancer risk – where do we stand in 2005? J Cell Mol Med. 2005; 9:208-221.
15. Crisostomo J, Matafome P, Santos-Silva D, Gomes AL, Gomes M, Patricio M, et al. Hyperresistinemia and metabolic dysregulation: a risky crosstalk in obese breast cancer. Endocrine. 2016; 53:433-442.
16. Patricio M, Pereira J, Crisostomo J, Matafome P, Gomes M, Seiça R, et al. Using Resistin, glucose, age and BMI to predict the presence of breast cancer. BMC Cancer. 2018; 18:18-29.
17. Paz-Filho G, Lim EL, Wong ML, Licinio J. Associations between adipokines and obesity-related cancer. Front Biosci. 2011; 16:1634-1650.
18. Steppan CM, Bailey ST, Bhat S, Brown EJ, Banerjee RR, Wright CM, et al. The hormone resistin links obesity to diabetes. Nature, 2001; 409: 307-312.
19. Das RN, Lee Y, Mukherjee S, Oh S. Relationship of body mass index with diabetes & breast cancer biomarkers. J Diab Manag. 2019; 9:163-168.
20. Kim J, Das RN, Lee Y, Sahoo RK. Association of monocyte chemoattractant protein-1 with age, glucose, BMI, insulin and other breast cancer biomarkers. Oncol Radiothep. 2019; 13: 5-9.
21. Das RN, Lee Y. Association of Serum Adiponectin with Age, BMI and Other Breast Cancer Biomarkers. J Blood Lymph 2018; 8:233.
22. Das RN, Lee Y. Association of resistin with BMI, age diabetes and breastcancer biomarkers. J Oncol Res Treat. 2019; 4:135.
23. Das RN, Lee Y. Relationship of leptin with glucose, BMI, age, insulin and breast cancer biomarkers. Arch Gen Intern Med. 2019; 3:1-3.
24. Lee Y, Nelder JA, Pawitan Y. Generalized Linear Models with Random Effects (Unified Analysis via H–likelihood). Chapman & Hall, London, 2017.
25. Das RN, Lee Y. Log-normal versus gamma models for analyzing data from quality-improvement experiments.  Quality Eng 2009; 21:79-87.
26. Lesperance ML, Park S. GLMs for the analysis of robust designsvwith dynamic characteristics. J Quality Tech 2003; 35:253-263.